a) Calculer la différence de potentiel EA – EB pour laquelle l’ion K+ est à l’équilibre.

Le mouvement d’un ion à travers une membrane perméable est dû :

    au potentiel chimique (force due à la différence de concentration de part et d’autre de la
    membrane) ;

    au potentiel électrique (force due à la différence de potentiel de part et d’autre de la
    membrane).

Le potentiel électrochimique d’un ion X de valence z est donné par la formule :

À l’équilibre électrochimique, la différence de potentiel électrochimique est nulle. La force due à la différence de potentiel s’oppose exactement à la force due à la différence de concentration entre les deux compartiments A et B séparés par la membrane.

La valeur de la différence de potentiel à l’équilibre est donnée par l’équation suivante, appelée équation de Nernst

pour une température de 29°C,

(pour calculer la valeur de RT/F, voir Constantes)
 

L’ion K+ à l’équilibre satisfait à l’équation de Nernst :

b) Pour cette différence de potentiel, quelle est la valeur du flux net de K+ ?

À l’équilibre, le flux net d’ion est nul.

Calculons le potentiel d’équilibre pour l’ion, en utilisant l’équation de Nernst.

b) Si l’ion n’est pas à l’équilibre, dans quel sens la force électrochimique va-t-elle le faire migrer ?

Le mouvement de l’ion dépend de la force électrochimique à laquelle il est soumis. La diffusion se fera dans le sens pour lequel la différence de potentiel électrochimique sera négative (transformation spontanée).

Le potentiel électrochimique d’un ion X de valence z est donné par la formule :

À l’équilibre, le potentiel électrochimique est nul.

Donc : z(E_A – E_B) < z(E_A – E_B)_eq

(E_A – E_B)_eq = + 60 mV z(E_A – E_B)_eq = - 60 mV

(E_A – E_B) = + 100 mV z(E_A – E_B) = - 100 mV

On appelle " membrane de Donnan " une membrane perméable à certaines particules chargées et pas à d’autres. C’est le cas ici, puisque la membrane est perméable à K⁺ et à Cl^-, mais pas à Y^-.

Que décrit l’équation de Gibbs-Donnan ?

L’équation de Gibbs-Donnan décrit l’état d’équilibre de chaque paire d’ions monovalents de part et d’autre d’une membrane de Donnan.

b) Les ions sont-ils à l’équilibre ?

Au départ, l’ion Cl^- n’est pas à l’équilibre, étant en excès dans le compartiment B. Le flux de Cl^- va aller de B vers A. Ce flux de charges négatives va créer une différence de potentiel négative ((E_A – E_B)<0), ce qui va provoquer un flux de K⁺ également de B vers A.

c) À l’équilibre, quelles seront les concentrations des différents ions dans chaque compartiment ?

À l’équilibre, K⁺ et Cl^- satisfont à l’équation de Gibbs-Donnan :

En remplaçant [K⁺]_A et [Cl^-]_A par leurs équivalents calculés à partir de (4) et (5), on obtient :

Quelle sera la différence de potentiel entre A et B ?

K⁺ et Cl^- étant à l’équilibre, ils satisfont à l’équation de Nernst. La différence de potentiel peut donc être calculée à l’aide de cette équation, à partir de l’un ou l’autre de ces deux ions.

E_A – E_B = - 60log ([K⁺]_A/[ K⁺]_B) = + 60log ([Cl^-]_A/[Cl^-]_B) (mV)

E_A – E_B = - 60log2

E_A – E_B = - 18 mV

Le potassium est-il à l’équilibre ?

Non, car les concentrations en K⁺ sont différentes dans les 2 compartiments et la différence de potentiel est nulle.

Sinon, dans quel sens se fera le flux de K+ ?

Dans le sens du gradient de concentration, c’est-à-dire de A vers B.

Quel effet ce flux aura-t-il sur le potentiel de part et d’autre de la membrane ?

Le flux va accumuler des charges positives sur la face B de la membrane, créant ainsi une différence de potentiel (E_A – E_B)<0)

À quelle valeur le potentiel se stabilisera-t-il ?

À la valeur du potentiel d’équilibre pour K⁺, soit E_A – E_B = – 60 mV.

b) deuxième cas : la membrane n’est perméable qu’à l’ion sodium.

Le sodium est-il à l’équilibre ?

Non, pour les mêmes raisons que K⁺.

Sinon, dans quel sens se fera le flux de Na⁺ ?

De B vers A.

Quel effet ce flux aura-t-il sur le potentiel de part et d’autre de la membrane ?

Le flux va accumuler des charges positives sur la face A de la membrane, créant ainsi une différence de potentiel (E_A – E_B)>0)

À quelle valeur le potentiel se stabilisera-t-il ?

À la valeur du potentiel d’équilibre pour Na⁺, soit E_A – E_B = + 60 mV.

c) troisième cas : la membrane est également perméable à K⁺ et à Na⁺.

À quelle valeur le potentiel se stabilisera-t-il ?

À la valeur intermédiaire entre le potentiel d’équilibre pour K⁺et pour Na⁺, soit 0 mV.

Pour cette valeur de potentiel, et ces concentrations, K⁺ et Na⁺ seront-ils à l’équilibre ?

Non, car le potentiel de membrane est différent des potentiels d’équilibre de chaque ion.

d) que peut-on en conclure sur la participation des ions à l’établissement d’un potentiel transmembraire ?

Le potentiel de membrane est la moyenne pondérée des potentiels d’équilibre de chaque ion auquel la membrane est perméable. Plus la membrane est perméable à un ion, plus le poids de cet ion dans l’établissement du potentiel de membrane sera important.
NB : D’un point de vue électrique, pour chaque ion, le facteur de pondération est la conductance membranaire relative pour cet ion (le calcul de la valeur du potentiel de membrane à partir des conductances relatives se fait à partir de l’équation de conductance, traitée dans l’exercice n°6).

L’équation de GHK permet de calculer la valeur du potentiel de membrane en fonction des concentrations intracellulaires et extracellulaires des ions K⁺, Na⁺ et Cl^-, et de leur perméabilité, selon la formule :

Si l’ion Cl- est à l’équilibre électrochimique, quelle est sa participation au potentiel de membrane ? Comment peut-on alors simplifier l’équation de GHK ?

Si l’ion Cl^- est à l’équilibre, distribué passivement de part et d’autre de la membrane, il ne participe pas au potentiel de membrane (rôle du chlore dans le potentiel de membrane). L’équation de GHK peut se simplifier ainsi :

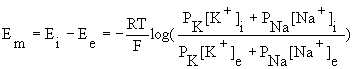
Les ions K⁺ et Na⁺ ne sont pas à l'équilibre électrochimique ;  le maintien du gradient de concentration de K⁺ et Na⁺se fait pas un mécanisme actif.

b) Calculez le potentiel de membrane de l’axone de calmar (on rappelle que, par convention, le potentiel de membrane E_m est le potentiel intracellulaire moins le potentiel extracellulaire (E_m = E_i – E_e)).

c) L’ouverture de canaux sodiques augmente la perméabilité au sodium ; P_Na = 20. Quelle est alors la valeur du potentiel de membrane ?

d) L’ouverture de canaux potassiques augmente considérablement la perméabilité au potassium. La perméabilité au sodium et au chlore devient négligeable par rapport à la perméabilité au potassium. Vers quelle valeur va alors tendre le potentiel de membrane ?

Le potentiel de membrane va tendre vers le potentiel d’équilibre pour le potassium, soit – 96 mV.

 
Pour un ion donné X, l’intensité du courant en fonction de E_m est donnée par la loi d’Ohm :

R_x.I_x = (E_m – E_x)

où R_x est la résistance à l’ion, I_x le courant porté par cet ion, E_x son potentiel d’équilibre. Si on exprime l’équation en fonction de la conductance à l’ion g_x, on obtient :

I_x = (E_m – E_x) g_x

 
Les courants ioniques à travers la membrane plasmique étant des courants en parallèle, le courant global I est la somme des courants ioniques.

I = S I_x = S (E_m – E_x) g_x

I = S E_m g_x – S E_x g_x

I = E_m S g_x – S E_x g_x

Puisqu’au repos, I = o, on obtient :

0 = E_m S g_x – S E_x g_x

S E_x g_x = E_mS g_x

E_m = (S E_x g_x )/S g_x E_m = S E_x (g_x /S g_x)                          équation de conductance de corde

où S g_x est la somme des conductances, et g_x /S g_x la conductance relative de chaque ion.

Le potentiel membranaire est donc égal à la somme des potentiels d’équilibre de chaque ion multipliés par la conductance relative de cet ion.

Pour le muscle étudié, on obtient donc :

E_m = E_Na(g_Na /S g_x) + E_K(g_K /S g_x) + E_Cl(g_Cl /S g_x)

E_m = 60(0,05) - 89(0,5) -89(0,45) mV

E_m = -81,6 mV
 

L’ouverture de canaux sodium augmente considérablement la conductance relative au sodium. Le potentiel membranaire va donc se rapprocher du potentiel d’équilibre de l’ion Na⁺.

E_Na = -60log([Na⁺]_i/[Na⁺]_e) = -60log(10/120) mV

E_Na = + 65 mV

b) Quelle est la conductance unitaire du canal ?

L’intensité du courant dépend de la conductance du canal et de la force électrochimique appliquée selon la loi d’Ohm U = R x I

(la conductance g, exprimée en Siemens (S) étant égale à l’inverse de la résistance R).

La force électromotrice correspond à la différence entre le potentiel membranaire E_m et le potentiel d’équilibre E_Na.

On a E_m < E_Na, donc zE_m < zE_Na Le flux de Na⁺ va du milieu extracellulaire vers le milieu intracellulaire. Le flux est entrant (cf. exercice n° 2 b)).

Na⁺ étant un cation, le flux d’ion et le courant associé sont de même signe. Le courant est un courant entrant, donc négatif.

Si (E_m - E_Na) est négatif, le courant est négatif aussi. Si le courant est porté par un cation, le flux d’ion est entrant. S’il est porté par un anion, le flux d’ion est sortant.
 

question subsidiaire :
d) quel est le nombre d’ions qui traversent le canal en 1 msec ?
1 A = 1C. sec^-1
charge élémentaire de l’électron e = 1,6 10^-19 C
1 A = 1C. sec^-1

La charge élémentaire de l’électron étant 1,6 10^-19 C, un C correspond à 1/(1,6.10^-19) charges élémentaires. 1 A est donc égal à 0,625.10¹⁹ charges élémentaires par seconde, 0,625.10¹⁶ charges élémentaires par milliseconde.

Le courant étant de 2.10^-12 A, il correspond à 2 x 0,625.10⁴ charges élémentaires par msec.

Na⁺ étant monovalent, le passage d’une charge élémentaire à travers le canal correspond au passage d’un ion.

En une milliseconde, il passe donc 12500 ions à travers un canal.

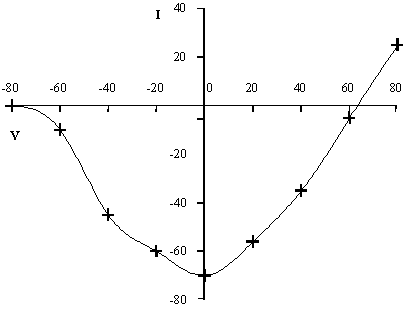
Le potentiel d’inversion du courant est de + 65 mV.

b) Les concentrations intracellulaire et extracellulaire en sodium de la cellule sont les suivantes : [Na⁺]_i = 10 mM [Na⁺]_e = 130 mM.

Calculez le potentiel d’équilibre du sodium. Que peut-on dire de la nature du courant étudié?

E_eq = -60 log(10/130) = + 67 mV.

Le potentiel d’équilibre de l’ion sodium est très proche du potentiel d’inversion du courant étudié. Il est probable que le courant en question soit un courant sodique.